Basic Neural Network

Posted on September 22, 2018 in deeplearning • 95 min read

A neural network written in Python, consisting of a single neuron that uses back propagation to learn.

Dependencies¶

None! Just numpy.

In [1]:

import numpy as np

Sigmoid Function¶

Sigmoid functions are used for clasifications of two classes, these function may have any value between 0 and 1. We use it to convert numbers to probablities. They also have several desirable properties for traning neural networks. Mathamatical Equation of Sigmoid Function : 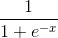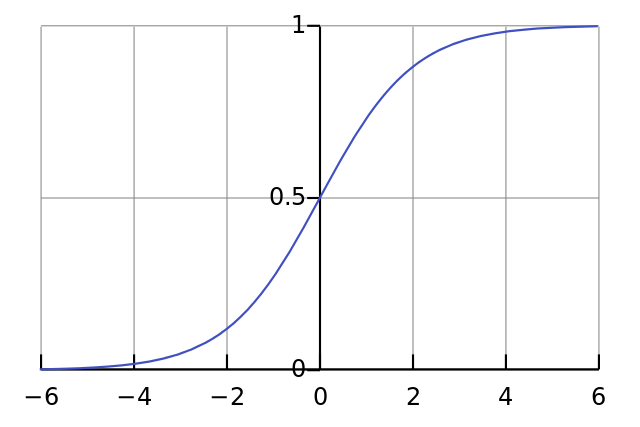One of the desirable properties of a sigmoid function is that its output can be used to create its derivative. If the sigmoid's output is a variable "out", then the derivative is simply out * (1-out). This is very efficient. If you're unfamililar with derivatives, just think about it as the slope of the sigmoid function at a given point

In [2]:

# sigmoid function
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)
    return 1/(1+np.exp(-x))

Input Dataset¶

Initialize our input dataset as numpy matrix.Each rows is a single "traning example". Each nodes corresponds to one of our input nodes.Thus we have 3 input nodes to the network and 4 training examples.

In [3]:

X = np.array([  [0,0,1],
                [0,1,1],
                [1,0,1],
                [1,1,1] ])

Output Dataset¶

This initialize our output dataset. In this case, we generated dataset horizontally (With a single row and 4 coloum)for space. ".T" is the transpose function. After the transpose, this y matrix has 4 rows with one column. Just like our input, each row is a training example, and each column (only one) is an output node. So, our network has 3 inputs and 1 output and storing output as

In [4]:

y = np.array([[0,0,1,1]]).T

In [5]:

# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)

Weight Matrix¶

This is our weight matrix for this neural network. It's called "syn0" to imply "synapse zero" (_**Synapse** : In the nervous system, a synapse is a structure that permits a neuron (or nerve cell) to pass an electrical or chemical signal to another neuron or to the target efferent cell._)

Since we only have 2 layers (input and output), we only need one matrix of weights to connect them. Its dimension is (3,1) because we have 3 inputs and 1 output. Another way of looking at it is that l0 is of size 3 and l1 is of size 1. Thus, we want to connect every node in l0 to every node in l1, which requires a matrix of dimensionality (3,1). :)

Another note is that the "neural network" is really just this matrix. We have "layers" l0 and l1 but they are transient values based on the dataset. We don't save them. All of the learning is stored in the syn0 matrix.

In [6]:

syn0 = 2*np.random.random((3,1)) -1

Calculating l1_delta by using "Error Weighted Derivative" Formula : 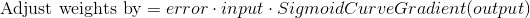So by substuting SigmoidCurveGradient(in our case nonlin(X,deriv=True)) we get

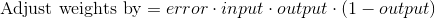
Some Methods used from numpy is as follows :

exp : the natural exponential
array : creates a matrix
dot : multiplies matrices
random : gives us random numbers

In [7]:

for itr in range(1000):
    # forward prapogation
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))
    
    #how much did we miss
    l1_error = y - l1
    #multiply how much we missed by the slope
    # of the sigmoid at the value l1
    l1_delta = l1_error * nonlin(l1,True)
    
    #update weights
    syn0 += np.dot(l0.T,l1_delta)
    
print("Output after training")
print(l1)

Output after training
[[0.03178421]
 [0.02576499]
 [0.97906682]
 [0.97414645]]

Complete Code¶

Complete code is available on github (https://github.com/avvineed/Basic-Neural-Network)